Using Fourier Transforms with the Web Audio API

The Web Audio API gives JavaScript programmers easy access to sound processing and synthesis. In this article, we will shine a light on custom oscillators, a little-known feature of the Web Audio API that makes it easy to put Fourier transforms to work to synthesize distinctive sound effects in the browser.

Web Audio Oscillators

The Web Audio API lets you compose a graph of audio elements to produce sound. An oscillator is one such element – a sound source that generates a pure audio signal. You can set its frequency and its type, which can be sine, square, sawtooth or triangle but, as we are about to see, there is also a powerful custom type.

First, let’s try a standard oscillator. We simply set its frequency to 440 Hz, which musicians will recognize as the A4 note, and we include a type selector to let you hear the difference between the sine, square, sawtooth and triangle waveforms.

See the Pen Web Audio oscillator by Seb Molines (@Clafou) on CodePen.

Custom oscillators let you define your own waveforms in place of these built-in types, but with a twist: they use Fourier transforms to generate this waveform. This makes them ideally suited for realistic sound generation.

Fourier Transforms By Example

The Fourier transform is the mathematical tool used by audio compression standards such as MP3, among many other applications. The inverse Fourier transform decomposes a signal into its constituent frequencies, much like the human ear processes vibrations to perceive individual tones.

At a high level, Fourier transforms exploit the fact that a complex signal can be decomposed into discrete sinusoidal curves of incremental frequencies. It works using tables of coefficients, each applied to a multiple of a fundamental frequency. The bigger the tables, the closer the approximation. Intrigued? The Wikipedia page is worth a look, and includes animations to help visualize the decomposition of a signal into discrete sine curves.

But rather than delve into the theory, let’s put this into practice by deconstructing a simple continuous sound: an air horn.

Synthesizing a Horn

For this article we will use this recording of a police siren and horn. A spectrograph of the horn sound, created using the open source audio editor Audacity, is shown here.

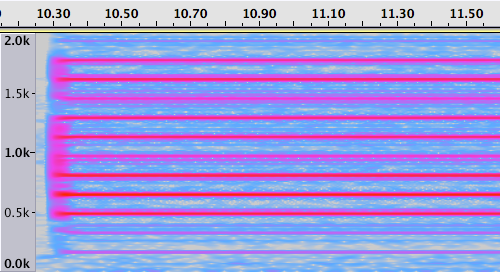
It clearly shows a number of lines of varying intensity, all spaced at equal intervals. If we look closer, this interval is about 160Hz.

Fourier transforms work with a fundamental frequency (let’s call it f) and its overtones, which are multiples of f. If we choose 160Hz as our fundamental f, the line at 320Hz (2 x f) is our first overtone, the line at 480Hz (3 x f) our second overtone, and so on.

Because the spectrograph shows that all lines are at multiples of f, an array of the intensities observed at each multiple of f is sufficient to represent a decent imitation of the recorded sound.

The Web Audio API documentation for createPeriodicWave, which creates a custom waveform from Fourier coefficients, tells us this:

The real parameter represents an array of cosine terms (traditionally the A terms). In audio terminology, the first element (index 0) is the DC-offset of the periodic waveform and is usually set to zero. The second element (index 1) represents the fundamental frequency. The third element represents the first overtone, and so on.

There is also an imag parameter that we can ignore as phases are irrelevant for this example.

So let’s create an array of these coefficients (estimating them to be 0.4, 0.4, 1 , 1 , 1 ,0.3, 0.7, 0.6, 0.5, 0.9, 0.8 based on the brightness of the lines on the spectrograph starting at the bottom). We then create a custom oscillator from this table and synthesize the resulting sound.

var audioContext = new AudioContext();
var osc = audioContext.createOscillator();

var real = new Float32Array([0,0.4,0.4,1,1,1,0.3,0.7,0.6,0.5,0.9,0.8]);

var imag = new Float32Array(real.length);
var hornTable = audioContext.createPeriodicWave(real, imag);

osc = audioContext.createOscillator();
osc.setPeriodicWave(hornTable);
osc.frequency.value = 160;
osc.connect(audioContext.destination);
osc.start(0);

See the Pen Custom oscillator: Horn by Seb Molines (@Clafou) on CodePen.

Not exactly a soothing sound, but strikingly close to the recorded sound. Of course, sound synthesis goes far beyond spectrum alone–in particular, envelopes are an equally important aspect of timbre.

From Signal Data to Fourier Tables

It is unusual to create Fourier coefficients by hand as we just did (and few sounds are as simple as our horn sound which is only composed of harmonic partials, i.e. multiples of f). Typically, Fourier tables are computed by feeding real signal data into an inverse FFT (Fast Fourier Transform) algorithm.

You can find Fourier coefficients for a selection of sounds in the Chromium repository, among which is the organ sound played below:

See the Pen Custom oscillator: Organ by Seb Molines (@Clafou) on CodePen.

The dsp.js open source library lets you compute such Fourier coefficients from your own sample data. We will now demonstrate this to produce a specific waveform.

Low-Frequency Oscillator: Police Siren Tone

A US police siren oscillates between a low and a high frequency. We can achieve this using the Web Audio API by connecting two oscillators. The first (a low-frequency oscillator, or LFO) modulates the frequency of the second which itself produces the audible sound waves.

To deconstruct the real thing, just as before, we take a spectrograph of a police siren sound from the same recording.

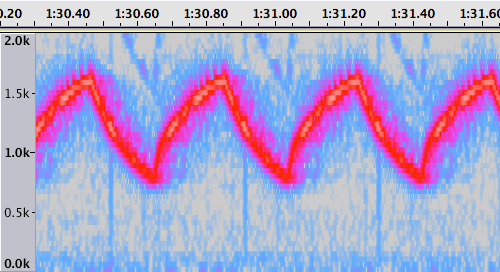
Rather than horizontal lines, we now see a shark fin-shaped waveform representing the rhythmic tone modulation of the siren. Standard oscillators only support sine, square, sawtooth and triangle-shaped waveforms, so we cannot rely on those to mimic this specific waveform. But we can create a custom oscillator once again.

First, we need an array of values representing the desired curve. The following function produces such values, which we stuff into an array called sharkFinValues.

See the Pen Waveform function for a siren tone modulation by Seb Molines (@Clafou) on CodePen.

Next, we use dsp.js to compute Fourier coefficients from this signal data. We obtain the real and imag arrays that we then use to initialize our LFO.

var ft = new DFT(sharkFinValues.length);
ft.forward(sharkFinValues);
var lfoTable = audioContext.createPeriodicWave(ft.real, ft.imag);

Finally, we create the second oscillator and connect the LFO to its frequency, via a gain node to amplify the LFO’s output. Our spectrograph shows that the waveform lasts about 380ms, so we set the LFO’s frequency to 1/0.380. It also shows us that the siren’s fundamental tone ranges from a low of about 750Hz to a high of about 1650Hz (a median of 1200Hz ± 450Hz), so we set the oscillator’s frequency to 1200 and the LFO’s gain to 450.

We can now start both oscillators to hear our police siren.

osc = audioContext.createOscillator();
osc.frequency.value = 1200;

lfo = audioContext.createOscillator();
lfo.setPeriodicWave(lfoTable);
lfo.frequency.value = 1/0.380;

lfoGain = audioContext.createGain();
lfoGain.gain.value = 450;

lfo.connect(lfoGain);
lfoGain.connect(osc.frequency);
osc.connect(audioContext.destination);

osc.start(0);
lfo.start(0);

See the Pen Siren by Seb Molines (@Clafou) on CodePen.

For more realism we could also apply a custom waveform to the second oscillator, as we have shown with the horn sound.

Conclusion

With their use Fourier transforms, custom oscillators give Web Audio developers an easy way to synthesize complex tones and to fully automate custom effects such as the siren waveform that we have demonstrated.

Sound synthesis is much more flexible than working with audio samples. For example it is easy to build on this siren effect to add more effects, as I did to add a Doppler shift in this mobile app.

The “Can I Use” spec shows that the Web Audio API is enjoying broad browser support, with the exception of IE. Not all browsers are up to date with the latest W3C standard, but a Monkey Patch is available to help write cross-browser code.

Android L will add Web Audio API support to the WebView, which iOS has been doing since version 6. Now is a great time to start experimenting!